Low Tide

Small Boat Stability

• Published Sunday, November 1st, 2015
• |Comments
• SubscribeRSS

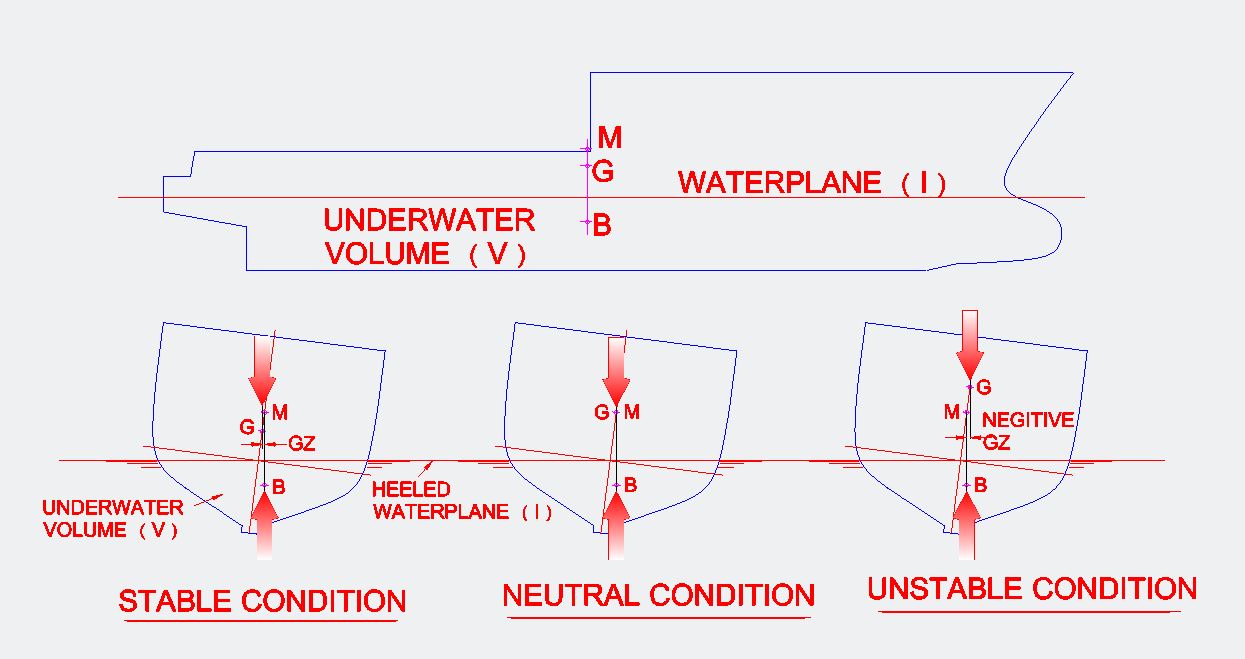
Before we start looking at specific stability issues and possible regulatory problems, it’s important to get the basics understood. Above is a basic diagram showing three stability cases. The “Stable Condition” where G is below M and there is a positive GZ. Gravity is pushing down through G, the Buoyancy force is pushing up through B, and there is a positive righting force. In the “Neutral Condition” the vessel could roll over either way, as there is no righting force or GZ. G and M are in the same place. Finally in the “Unstable Condition” G is above M and there is a negative GZ working to heel the vessel even further.

Hydrostatic Nomenclature

B or CB – Center of Buoyancy, the center through which the buoyant force acts. The CB moves as the underwater shape changes as the hull moves up and down (or rolls sideways) in the water. If the hull is floating free to trim or roll, the CB will always be directly under the center of gravity. During launching this doesn’t happen because the hull is “aground” forward.
M – Metacenter, the theoretical point around which the boat rolls or trims. There are separate transverse and longitudinal M’s.
K – Keel or baseline, the fixed line from which all vertical measurements are taken.
G – Center of Gravity of the vessel. The center of all the various weights that make up the boat. Addressed separately as VCG (Vertical Center of Gravity), LCG (Longitudinal Center of Gravity), and TCG (Transverse Center of Gravity). In computerese X is longitudinal, Y is athwartships, and Z is vertical.
GM – Distance from G to M in ft. or metres. Considered a general indication of a given vessel’s stability. To be stable G must be below M. A larger GM means the ship is stiff, a small GM (say less than one ft) is a tender vessel, a negative GM indicates an unstable ship.
GZ – Righting Arm in feet or metres. A horizontal distance between the CG acting downward and the CB acting upward.
V – Volume of the hull (underwater portion) in cubic feet or metres. The displaced volume (underwater) will be equal to the total weight of the vessel divided by the weight of the water she’s floating in. So if your boat weighs 5000 pounds(2273Kg) on the trailer, afloat she will displace 5000 pounds(2273Kg). Seawater weighs approximately 64 pounds(29Kg) per cubic foot so underwater volume (V) is 5000/64 = 78.1 cubic feet, or 2273/1000 = 2.27 cubic metres.
I – Inertia of Waterplane. The waterplane is a cut through the hull at the waterline. The distribution of this area affects stability. A barge and a needleboat could have the same waterplane area, but very different stability.
BM = I/V – Key stability equation. Inertia of the waterplane (I), divided by the displacement (V), is equal the distance from (B) the center of buoyancy, to (M) the meta center.
Ultimate Stability Angle- Called the angle of vanishing stability, this is the heel angle where righting force is zero.
Downflooding Angle- The heel angle where water starts coming through some hull opening (doors, windows, ports, hatches) and degrades stability of the vessel.
Free Surface- When the contents of a tank (fuel, fresh water, wet fish) slosh to one side it sets up a heeling force, which can degrade stability.